Last Updated: February 23, 2006
Michael Ligh (michael.ligh@mnin.org)
This is an overview of the SSH2 protocol, with a focus on how it uses cryptography to accomplish many of its goals: authentication, integrity, and confidentiality. The information is derived from client-side debug output; a network packet capture; protocol decoding by Ethereal; RFC drafts for SSH-ARCH, SSH-TRANS, SSH-AUTH, SSH-CONN; O'Reilly's Secure Shell Definitive Guide, VPNs Illustrated, and Practical Cryptography. The expected product of the guide is an ability to detect insecure client and/or server settings and recognize anomalies during session establishment. The sections are organized by order of which they occur during an SSH2 login.
|
|
Packet No(s) |
|
|
|
1-3 |
|
|
|
4-5 |
|
|
|
6-7 |
|
|
|
|
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
- |
|
|
|
- |
|
|
|
|
|
|
|
- |
|
|
|
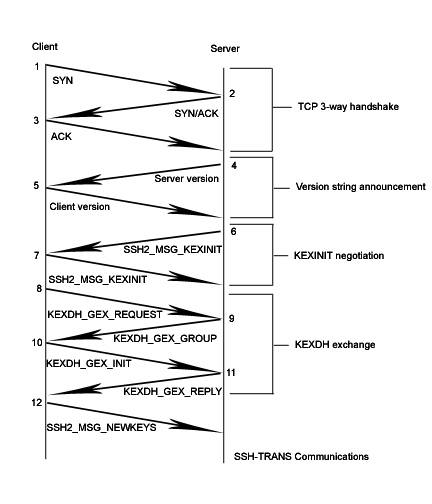
Note: This diagram is modeled after the conventions used in Richard Steven's TCP/IP Illustrated. With client on the left and server on the right, time progresses as packets move from top to bottom. Packets are numbered at the base of the arrow on the sender's side. Traffic in sections 1, 2, and 3 are plain text. Communications are not encrypted until after the SSH2_MSG_NEWKEYS is sent. |
In this example, host .14 (the client) establishes a TCP connection to port 22 of host .11 (the server), the two sides announce SSH versions, and the key exchange initialization takes place. For brevity, the 3-way handshake is the only sub-section in which either side's acknowledgment (ACK) packets affect the packet count. Following section 1, the two peers will have derived the following information:
If you're reading this, then likely you already know the significance of the 3-way handshake. It is provided here to be complete. Using the -v option when calling the SSH client on .14, these three packets produce the output:
debug1: Connecting to 192.168.1.11 [192.168.1.11] port 22. debug1: Connection established.
The network packet captures in this document are recorded with Ethereal. Here are the first three:
/* Packets 1, 2, and 3 */ 192.168.1.14.55821 > 192.168.1.11.22: S 381470515:381470515(0) win 5840 192.168.1.11.22 > 192.168.1.14.55821: S 1684940992:1684940992(0) ack 381470516 win 5792 192.168.1.14.55821 > 192.168.1.11.22: . ack 1 win 1460
There are two main, incompatible, versions of the SSH protocol: SSH1 (1.5) and SSH2. Most recent implementations still support both protocols, though support for the older, less secure SSH1 version should not be used. One major reason is because SSH1 only applies a CRC32 (cyclancy redundancy check) to the message for integrity, rather than a MAC (message authentication code). CRCs are not collision-resistant functions and are normally just used to detect accidental errors in transmissions (IP, TCP, and UDP, for example, use a checksum in their headers). MACs, on the other hand, are strengthened by using a cryotographic hash such as MD5 or SHA1.
|
Note: by definition, hashes produce a fixed length output. Due to MD5's 128-bit output, a collision can be produced every 2^64 computations of the function. SHA1 creates a 160-bit value, which makes it magnitudes more difficult (2^80) to produce a collision. Although SHA256 would be even more secure, all of these are a world apart from CRC32. |
In this sub-section, two packets are exchanged. The server sends it's protocol version first and the client replies with it's own version. A special code "1.99" specifies that the sender supports both SSH1 and SSH2. In our example, the client and server both suport SSH2 only.
debug1: Remote protocol version 2.0, remote software version OpenSSH_4.1 debug1: match: OpenSSH_4.1 pat OpenSSH* debug1: Enabling compatibility mode for protocol 2.0 debug1: Local version string SSH-2.0-OpenSSH_4.2
If the protocol versions are compatible, the connection progresses to the next step. If they are not, then either peer can force a termination. View the packet capture for a closer look at the traffic that produces the above output.
/* Packet 4 */
Internet Protocol, Src: 192.168.1.11 (192.168.1.11), Dst: 192.168.1.14 (192.168.1.14)
Transmission Control Protocol, Src Port: 22 (22), Dst Port: 55821 (55821), Seq: 1, Ack: 1, Len: 20
SSH Protocol
Protocol: SSH-2.0-OpenSSH_4.1\n
0000 00 0c 29 6d 5c 01 00 50 2c 05 6b a9 08 00 45 00 ..)m\..P,.k...E.
0010 00 48 55 20 40 00 40 06 62 26 c0 a8 01 0b c0 a8 .HU @.@.b&......
0020 01 0e 00 16 da 0d 64 6e 28 c1 16 bc c7 34 80 18 ......dn(....4..
0030 05 a8 67 ce 00 00 01 01 08 0a 0b 79 7d e4 04 99 ..g........y}...
0040 fe e0 53 53 48 2d 32 2e 30 2d 4f 70 65 6e 53 53 ..SSH-2.0-OpenSS
0050 48 5f 34 2e 31 0a H_4.1.
/* Packet 5 */
Internet Protocol, Src: 192.168.1.14 (192.168.1.14), Dst: 192.168.1.11 (192.168.1.11)
Transmission Control Protocol, Src Port: 55821 (55821), Dst Port: 22 (22), Seq: 1, Ack: 21, Len: 20
SSH Protocol
Protocol: SSH-2.0-OpenSSH_4.2\n
0000 00 50 2c 05 6b a9 00 0c 29 6d 5c 01 08 00 45 00 .P,.k...)m\...E.
0010 00 48 39 d6 40 00 40 06 7d 70 c0 a8 01 0e c0 a8 .H9.@.@.}p......
0020 01 0b da 0d 00 16 16 bc c7 34 64 6e 28 d5 80 18 .........4dn(...
0030 05 b4 66 ae 00 00 01 01 08 0a 04 99 fe e0 0b 79 ..f............y
0040 7d e4 53 53 48 2d 32 2e 30 2d 4f 70 65 6e 53 53 }.SSH-2.0-OpenSS
0050 48 5f 34 2e 32 0a H_4.2.
The primary objective of this round-trip exchange is to negotiate the algorithms for key exchange, bulk data encryption, message integrity, and compression. The peers will also let each other know the accepted host key types. In this stage they present their supported and preferred methods for the aforementioned functions in comma seperated list form. Preferred values are distinguished by placing them first in the list.
debug1: SSH2_MSG_KEXINIT sent debug1: SSH2_MSG_KEXINIT received debug1: kex: server->client aes128-cbc hmac-md5 none debug1: kex: client->server aes128-cbc hmac-md5 none
Two of the common key exchange methods are represented as diffie-hellman-group-exchange-sha1 and diffie-hellman-group1-sha1. The later method is less secure, because it uses a fixed group with which to make it's calculations. If diffie-hellman-group-exchange-sha1 (otherwise known as DHGEX) is selected, the group to use is negotiated based on the client's minimum, maximum, and preferred size prime modulus; from which the server chooses an appropriate value (see the SSH2_MSG_KEXDH_GEX_GROUP message in packet 9).
For bulk data encryption, SSH uses a symetric algorithm to scramble the message. Asymetric algorithms are simply not efficient when applied to bulk data, because they are too slow. The key used for this function is then encrypted with the peer's public host key to ensure that only a host with the corresponding private key can reproduce it. Without knowing the symetric algorithm key, the original message itself cannot be decrypted. So, upon receipt of the packet, a peer would use it's private key to decrypt the symetric algorithm key; and then use that resulting value to derive the plaintext message.
For data integrity, the two peers agree to use a common MAC algorithm. Encryption alone does not prove to the recipient that the remote peer truly generated and sent a message, and further more it does not prevent against alteration of the data. In fact, encryption does not even attempt to do this - it assumes the data will be available to anyone, and just makes it's best attempt to prevent it from being readable. MACs fill in this void by computing a hash of the unencrypted message body, a shared secret, and a session sequence number; which is then sent to the recipient. The shared secret is a product of the Diffie Hellman key exchange (section 2) and is computed individually by each peer, without needing to transmit over the network.
Without the MAC, an eavesdropper (man in the middle) could capture parts of the encrypted conversation (though not necessarily be able to read it) and conduct a replay attack, where s/he duplicates and resends that part of the converstation at a later point in time. The packet would still contain a payload signed with the recipient's public key, and the message would be encrypted with the expected symetric algorithm key; thus it would seem quite reasonable to the recipient. The session sequence number here is critical. It begins at 0 and increments by 1 for each message. Since this is a factor in the computation of the MAC value, only the sender can produce a legitimate code; and the recipient will only accept each code once - in the proper order. The MAC is not included in packets until after the SSH2_MSG_NEWKEYS is sent (packet 12).
SSH optionally will compress transmissions for more efficient delivery. Zlib is the only supported scheme according to the RFCs, but they are only drafts so this is subject to change. In the case that compression is negotiated, it is applied only to the message body and occurs before any MAC or encryption routines. Notice above that the client->server and server->client algorithms match; they both have chosen the same bulk data, integrity, and compression methods. This may be the case here, but it is not required. Data flow in both directions is independent of each other. The server could encrypt it's messages with AES128 and compress it with zlib, and the client could encrypt it's replies with 3DES with no compression.
Additionally, in this sub-section, the client and server both generate a sequence of 16 random bytes known as a cookie. This value is used in the key generation process, to ensure that neither side can completely determine the keys on it's own.
This section involves key exchange, using the selected Diffie Hellman protocol. By using this method properly, the two peers can derive the same secret key through plain text communications, without the possibility of eavesdroppers being able to calculate the same value. DH is not a total package solution, because it does not prevent man-in-the-middle data alteration. This attack will be described shortly. Following section 2, the peers will have derived the following information:
As mentioned earlier, if diffie-hellman-group-exchange-sha1 is selected as the key exchange method, the client notifies the server of it's minimum, preferred, and maximum prime size for the group. As the debug output shows, the numers are 1024, 1024, and 8192, respectively. The 32-bit unsigned integers have been highlighted below.
debug1: SSH2_MSG_KEX_DH_GEX_REQUEST(1024<1024<8192) sent debug1: expecting SSH2_MSG_KEX_DH_GEX_GROUP
Internet Protocol, Src: 192.168.1.14 (192.168.1.14), Dst: 192.168.1.11 (192.168.1.11)
Transmission Control Protocol, Src Port: 55821 (55821), Dst Port: 22 (22), Seq: 733, Ack: 661, Len: 24
SSH Protocol
SSH Version 2
Packet Length: 20
Padding Length: 6
Key Exchange
Msg code: Diffie-Hellman GEX Request (34)
Payload: 000004000000040000002000
Padding String:
0000 00 50 2c 05 6b a9 00 0c 29 6d 5c 01 08 00 45 00 .P,.k...)m\...E.
0010 00 4c 39 d8 40 00 40 06 7d 6a c0 a8 01 0e c0 a8 .L9.@.@.}j......
0020 01 0b da 0d 00 16 16 bc ca 10 64 6e 2b 55 80 18 ..........dn+U..
0030 06 f4 e6 6e 00 00 01 01 08 0a 04 99 fe e3 0b 79 ...n...........y
0040 7d f0 00 00 00 14 06 22 00 00 04 00 00 00 04 00 }......"........
0050 00 00 20 00 00 00 00 00 00 00 .. .......
This is the server's response to the SSH2_MSG_KEXDH_GEX_REQUEST. From the available options, the server selects an appropriate size for the group's prime and informs the client. This packet also contains two multiprecision integers containing the prime to be used (p) and the corresponding generator (g). After receiving this message, both peers know the DH group to use. There are only two remaining packets in the key exchange (packets 10 and 11) before enough parameters are negotiated to start encrypting data..
Internet Protocol, Src: 192.168.1.11 (192.168.1.11), Dst: 192.168.1.14 (192.168.1.14)
Transmission Control Protocol, Src Port: 22 (22), Dst Port: 55821 (55821), Seq: 661, Ack: 757, Len: 152
SSH Protocol
SSH Version 2
Packet Length: 148
Padding Length: 8
Key Exchange
Msg code: Diffie-Hellman Key Exchange Reply (31)
Payload: 0000008100CAADDDEC1667FC68B5FA15D53C4E1532DD2456...
Padding String:
0000 00 0c 29 6d 5c 01 00 50 2c 05 6b a9 08 00 45 00 ..)m\..P,.k...E.
0010 00 cc 55 2a 40 00 40 06 61 98 c0 a8 01 0b c0 a8 ..U*@.@.a.......
0020 01 0e 00 16 da 0d 64 6e 2b 55 16 bc ca 28 80 18 ......dn+U...(..
0030 07 0c 19 0a 00 00 01 01 08 0a 0b 79 7d f1 04 99 ...........y}...
0040 fe e3 00 00 00 94 08 1f 00 00 00 81 00 ca ad dd ................
0050 ec 16 67 fc 68 b5 fa 15 d5 3c 4e 15 32 dd 24 56 ..g.h....jN.2.$V
0060 1a 1a 2d 47 a1 2c 01 ab ea 1e 00 73 1f 69 21 aa ..-G.,.....s.i!.
0070 c4 07 42 31 1f df 9e 63 4b b7 13 1b ee 1a f2 40 ..B1...cK......@
0080 26 15 54 38 9a 91 04 25 e0 44 e8 8c 83 59 b0 10 &.T8...%.D...Y..
0090 f5 ad 2b 80 e2 9c b1 a5 b0 27 b1 9d 9e 01 a6 f6 ..+......'......
00a0 3a 6f 45 e5 d7 ed 2f f6 a2 a0 08 50 50 a7 d0 cf :oE.../....PP...
00b0 30 7c 3d b5 1d 24 90 35 59 07 b4 42 7c 23 a9 8d 0|=..$.5Y..B|#..
00c0 f1 eb 8a be f2 ba 20 9b b7 b0 df d8 bb 00 00 00 ...... .........
00d0 01 02 00 00 00 00 00 00 00 00 ..........
In this sub-section, the client computes a value based on p and g and sends it to the server. In particular, the client generates a random number x, such that 1 < x < (p-1)/2 and then calculates e = g^x mod p. In the below packet capture, you can see "e" being sent to the server, sandwiched between one 0x20 and six 0x00 bytes. The 0x20 (decimal 32) specifies the message type, which is Diffie-Hellman GEX Init in this case. This is important to note, because a message type of 0x20 with an inconsistent payload might be indication of some type of attack or reconnassance.
debug1: SSH2_MSG_KEX_DH_GEX_INIT sent debug1: expecting SSH2_MSG_KEX_DH_GEX_REPLY
Internet Protocol, Src: 192.168.1.14 (192.168.1.14), Dst: 192.168.1.11 (192.168.1.11)
Transmission Control Protocol, Src Port: 55821 (55821), Dst Port: 22 (22), Seq: 757, Ack: 813, Len: 144
SSH Protocol
SSH Version 2
Packet Length: 140
Padding Length: 6
Key Exchange
Msg code: Diffie-Hellman GEX Init (32)
Payload: 000000803DEEBF549A8BBA70F9B4E3DFB149ED844D67C1AD...
Padding String:
0000 00 50 2c 05 6b a9 00 0c 29 6d 5c 01 08 00 45 00 .P,.k...)m\...E.
0010 00 c4 39 d9 40 00 40 06 7c f1 c0 a8 01 0e c0 a8 ..9.@.@.|.......
0020 01 0b da 0d 00 16 16 bc ca 28 64 6e 2b ed 80 18 .........(dn+...
0030 08 34 2d 8a 00 00 01 01 08 0a 04 99 fe e5 0b 79 .4-............y
0040 7d f1 00 00 00 8c 06 20 00 00 00 80 3d ee bf 54 }...... ....=..T
0050 9a 8b ba 70 f9 b4 e3 df b1 49 ed 84 4d 67 c1 ad ...p.....I..Mg..
0060 6a 3c 6d b6 4a e2 99 65 37 a6 d6 b5 66 f0 39 d3 jkm.J..e7...f.9.
0070 15 ff d2 26 ca ac 96 c5 8b bb f2 5d 0d 39 36 69 ...&.......].96i
0080 1d 4b 2e 41 80 44 e2 50 dd 52 50 06 a3 1c bc 0e .K.A.D.P.RP.....
0090 dd 20 90 44 69 1a 4a f6 bf a0 6d 9d 4d 8a d2 a2 . .Di.J...m.M...
00a0 0f c0 1e e4 15 2a 8d c2 ee 6b cd 33 bb da 74 c1 .....*...k.3..t.
00b0 54 45 ad b6 9b 48 db 7b 6a 53 b7 b3 f4 45 21 96 TE...H.{jS...E!.
00c0 50 ee 22 95 21 97 7b 9d ff 9d 60 cf 00 00 00 00 P.".!.{...`.....
00d0 00 00 ..
Upon receipt of the client's SSH2_MSG_KEXDH_GEX_INIT message, the server generates it's own random number y, calculates f = g^y mod p, and sends "f" to the client. It also calculates k = e^y mod p, which is the value of the shared secret. The client does the same, using formula k = f^x mod p. If everything goes right, the client and server should compute identical values for k. This is very important, because k is one of the elements used to create the exchange hash signature, which is the primary factor in server authentication.
The exchange hash is created by contatenating several pieces of the puzzle, one of which is the value of k. It is also built with e, f, and data such as the client and server's version strings. Once collected, the combined data is run through the negotiated hashing algorithm, which is then signed with the server's private key. Included in this same packet is the server's public key.
|
Note: p, g, e, and f are all transmitted in plain text across the network, thus security of the system must not rely on secrecy of any of these values - they must all be considered known. In simple terms, the strength of DH is based on the fact that an attacker does not know x or y. If the shared secret k can only be computed as either k = e^y mod p or k = f^x mod p, the attacker is left empty handed. Note: based on the above information, an eavesdropper cannot determine x or y. However, a man in the middle could still alter the packets that contain e and f so that e = f = 1. If e and f equal 1, then the security of the system evaporates and an attacker can learn the value of k with ease. |
The first time .14 connects to .11, this public key is recorded in the client's known_hosts database (~/.ssh/known_hosts), which is then used in comparison against the key sent by the server on future connections. If the key does not match, then the client assumes he has never connected to this server before and prompts for permission to add it. If the public key does match, it is used to decrypt the exchange hash signature. In turn, the result is then compared to the client's own hash value for the same group of concatenated puzzle pieces. In the event that there is a match, the client concludes with strong certainty that a) the server possesses the private key that is paired with a pre-authorized public key and b) the server must know the value of shared secret k. At this point, the server has been authenticated.
It would be mighty dangerous if the client failed to check for an existing public key in it's known_hosts file. Consider the repercussions over an example. Assume an attacker compromises .12, and then sabotages DNS so that .11's DNS name now points to .12. He can now cause .14 to try logging into the wrong machine. Upon connecting, if the host key provided by .12 is not already in known_hosts, the client should produce a banner that warns of potential attack (mitm or redirection). However, if this check was not conducted and password authentication was enabled, the user at .14 would then unknowingly enter his credentials into the compromised .12 system, where the attacker could capture it. Since the server is the first one with an opportunity to exploit a trust relationship, the protocol was designed with these checks so that the client can properly authenticate the server first.
Here is the client side debug that relates to these few actions:
debug1: Host '192.168.1.11' is known and matches the RSA host key. debug1: Found key in /home/michali/.ssh/known_hosts:1 debug1: ssh_rsa_verify: signature correct
If the server's public key was not in known_hosts upon connection, a user would see the following error (or something similar - it can be personalized):
The authenticity of host '192.168.1.11 (192.168.1.11)' can't be established. RSA key fingerprint is 94:ed:a5:9f:80:ac:7c:25:02:d1:a6:5a:1d:84:02:bc. Are you sure you want to continue connecting (yes/no)? no Host key verification failed.
So back to the real example at this point all the required information for key generation has been negotiated. Using the shared secret, exchange hash, and session ID (which is the initial exchange hash), the peers calculate keys for the following purposes:
|
Note: the initial IV (initialization vector) is not required if the bulk data encryption routine is a stream cipher; SSH only requires them for block ciphers such as 3DES or AES. A nonce-generated or DH-negotiated (as opposed to a fixed, counter, or random) IV should ensure that two identical blocks of plain text will not produce identical cipher text blocks when encrypted with the same algorithm and the same key. |
Internet Protocol, Src: 192.168.1.11 (192.168.1.11), Dst: 192.168.1.14 (192.168.1.14)
Transmission Control Protocol, Src Port: 22 (22), Dst Port: 55821 (55821), Seq: 813, Ack: 901, Len: 464
SSH Protocol
SSH Version 2
Packet Length: 444
Padding Length: 10
Key Exchange
Msg code: Diffie-Hellman GEX Reply (33)
Payload: 00000095000000077373682D727361000000012300000081...
Padding String:
MAC String:
0000 00 0c 29 6d 5c 01 00 50 2c 05 6b a9 08 00 45 00 ..)m\..P,.k...E.
0010 02 04 55 2c 40 00 40 06 60 5e c0 a8 01 0b c0 a8 ..U,@.@.`^......
0020 01 0e 00 16 da 0d 64 6e 2b ed 16 bc ca b8 80 18 ......dn+.......
0030 07 0c b2 99 00 00 01 01 08 0a 0b 79 7d f5 04 99 ...........y}...
0040 fe e5 00 00 01 bc 0a 21 00 00 00 95 00 00 00 07 .......!........
0050 73 73 68 2d 72 73 61 00 00 00 01 23 00 00 00 81 ssh-rsa....#....
0060 00 de 38 1b a2 9a 31 65 d5 2e f2 62 a7 64 6b 98 ..8...1e...b.dk.
0070 15 6a 44 29 90 97 f2 db 61 f0 c7 46 26 f6 e7 b5 .jD)....a..F&...
0080 a5 cc 5f 92 e0 f2 b9 40 27 3f e7 46 d3 23 dd f0 .._....@'?.F.#..
0090 d9 1f f0 89 bc 14 a2 75 de 87 9b 2c fd c3 9d 90 .......u...,....
00a0 66 3a 2c 68 2a 0a 39 0e 64 cc 9b 04 d9 00 67 bf f:,h*.9.d.....g.
00b0 f5 93 34 19 70 92 86 cb a6 00 dc b8 eb 85 e0 ba ..4.p...........
00c0 d8 ea ce 4d 95 c0 4f f5 ea f5 2a e1 06 d1 1c e1 ...M..O...*.....
00d0 f0 be e9 2c d1 65 22 1f c9 0a 57 2f 57 bf 12 b3 ...,.e"...W/W...
00e0 8b 00 00 00 80 04 79 1d a8 49 7c e9 f2 d7 3e e9 ......y..I|...>.
00f0 af cc 03 31 26 ee 88 ed a2 e5 5c 08 f8 54 83 ae ...1&.....\..T..
0100 4c eb 7e 02 d4 43 44 4e 1e 19 55 32 c4 9d 45 e1 L.~..CDN..U2..E.
0110 87 42 d8 92 1b 96 41 d9 d7 43 e2 f0 46 69 b4 4e .B....A..C..Fi.N
0120 3a 2d 63 7f 40 24 a9 ec a1 71 13 37 eb 11 cd 21 :-c.@$...q.7...!
0130 a6 0c b5 ab 0d 3b f6 a9 1c c0 2a 1f 0d 06 5c d5 .....;....*...\.
0140 f5 79 4c 44 c3 0c 70 d6 c2 e2 dd b2 c0 5c 86 84 .yLD..p......\..
0150 d0 e8 57 58 fd 09 89 bb b6 dd 58 41 81 ef 70 ca ..WX......XA..p.
0160 75 39 f5 c5 78 00 00 00 8f 00 00 00 07 73 73 68 u9..x........ssh
0170 2d 72 73 61 00 00 00 80 6f c0 7e 21 bb 62 22 8e -rsa....o.~!.b".
0180 86 62 b1 89 08 02 ee 7c 24 c0 a7 ec 93 40 54 71 .b.....|$....@Tq
0190 76 23 26 47 f1 20 35 cd d8 4f d9 d7 ae 99 96 42 v#&G. 5..O.....B
01a0 b5 67 aa c9 7b b8 fb ce d9 b5 d2 1d 4c 4b e2 d2 .g..{.......LK..
01b0 03 37 1c d3 61 e6 fc 0c e5 f7 fa a3 da 1c 74 8f .7..a.........t.
01c0 03 82 ed 27 40 ca a4 e8 57 3f c3 d8 30 77 f3 69 ...'@...W?..0w.i
01d0 ad 74 06 72 85 60 c2 82 7d 52 9d 14 2f cc 43 06 .t.r.`..}R../.C.
01e0 a3 a9 e4 52 fb 00 55 a4 13 64 e2 00 66 7b db 15 ...R..U..d..f{..
01f0 02 a4 6f d1 f1 f2 31 23 00 00 00 00 00 00 00 00 ..o...1#........
0200 00 00 00 00 00 0c 0a 15 00 00 00 00 00 00 00 00 ................
0210 00 00 ..
Once the above operations are complete, the client sends it's SSH2_MSG_NEWKEYS message to the server. This is a notice that keying materials and algorithms should go into effect from this point on. Here is the client-side debug output:
debug1: SSH2_MSG_NEWKEYS sent debug1: expecting SSH2_MSG_NEWKEYS debug1: SSH2_MSG_NEWKEYS received
During the SSH session, either side can invoke a rekeying procedure. The RFC draft recommends this be done once per GB of data transferred or hour of activity, whichever comes first. This would make it more difficult for an attacker to obtain enough ciphertext to attempt cryptanalysis. It also prevents the 32-bit sequence number (a value used in MAC generation) from wrapping around back to zero, which would cause replay-attack vulnerabilities. The sequence number itself is never sent across the network, it is simply known by both peers based on how many messages have been exchanged.
Internet Protocol, Src: 192.168.1.14 (192.168.1.14), Dst: 192.168.1.11 (192.168.1.11)
Transmission Control Protocol, Src Port: 55821 (55821), Dst Port: 22 (22), Seq: 901, Ack: 1277, Len: 16
SSH Protocol
SSH Version 2
Packet Length: 12
Padding Length: 10
Key Exchange
Msg code: New Keys (21)
Padding String:
0000 00 50 2c 05 6b a9 00 0c 29 6d 5c 01 08 00 45 00 .P,.k...)m\...E.
0010 00 44 39 da 40 00 40 06 7d 70 c0 a8 01 0e c0 a8 .D9.@.@.}p......
0020 01 0b da 0d 00 16 16 bc ca b8 64 6e 2d bd 80 18 ..........dn-...
0030 09 74 04 f1 00 00 01 01 08 0a 04 99 fe e9 0b 79 .t.............y
0040 7d f5 00 00 00 0c 0a 15 00 00 00 00 00 00 00 00 }...............
0050 00 00 ..
Once an encrypted transport layer is established and identity of the server is verified, the client must authenticate. If you had doubts on why the server must be authenticated first, now it makes sense. If the client authenticates first then it would either do so in plain text or it would send credentials to a server it isn't familiar with (and thus shouldn't trust).
|
Note: SSH-AUTH itself does not do any encrypting or protecting of credentials. SSH-AUTH operates solely in plain text; it relies on the SSH-TRANS module to have previously secured the communication line. |
Since this document is focused on the cryptography of SSH2, only public key will be discussed in this section. The process is similar to how the server is authenticated using (public) host keys in section 2. A signature is created by concatenating several pieces of information known by both peers (strings, byte, and Boolean types in this case). The client then signs this data with the user's RSA or DSS private key. This resulting value is sent to the server along with the user's public key so the signature can be verified. If this checks out, then the client is believed to posess the private key of the corresponding public key sent in the packet; however this is only part of the login process. The more important aspect is confirming that the user who posesses this key pair is actually authorized to log in.
The SSH-AUTH module does not dictate how the later aspect should be conducted, rather it leaves this up to the particular implementation. The most common technique is to locate the users's advertised public key in the local users' authorized_keys file (~/.ssh/authorized_keys). This means each user who intends to authenticate via public key must have prior access to the server in order to plant the public key, which can be a considerable amount of work if many servers need to be accessed. This is why the solution is left up to the implementation - a centralized source such as an LDAP database or PKI key server can be queried for this information.
Aside from the cryptography, there are many other ways to satisfy a server's authentication requirements (assuming the server offers more than just the public key method) and even more ways to authorize a user's actions. Authentication is not the same as authorization. For example, a user might pass authentication (ie s/he is who s/he claims to be), but fail authorization (ie s/he is only allowed to run certain commands remotely). SSH2 can enforce rules such as where a user logs in from, commands s/he can execute; if X11 forwarding, port forwarding, or psuedo-terminals are allowed; and it can even chroot users to specific directories. At this point, SSH-CONN is normally invoked to handle the pty, multiplexing, and launch subsystems (sftp).
From the given information, it's evident that the security of SSH2 is based just as heavily on the security of underlying cryptosystems as it is on user interaction. If a user exposes his password and/or private key, the use of strong cryptography is wasted. Likewise, if a server supports weak algorithms and allows SSH1, a user can be as careful as possible, but the total system is still relatively insecure. In this section, some best practices will be discussed so administrators can choose what is right for their environment.
If password authentication is chosen as a standard, then the only credentials used to authenticate a user are sent (encrypted, of course) across the network from client to server. If public key authentication is chosen, neither the private key nor the associated passphrase leave the client. So, on one hand, the only piece an attacker needs is transmitted; and on the other hand neither piece is transmitted. At first glance, it might seem like a simple decision, but there is much more.
Password aging can easily be enforced on the server where SSH runs, while key pairs are less likely to be changed at regular intervals. If an attacker obtained a private key, he would be able to access the server for a much longer period before a switch locked him out. If a central source such as LDAP or PKI was available, key pairs could change more frequently without much work; but this isn't always possible.
Attackers wishing to circumvent security by sniffing a password would have to stage a mitm or similar type of attack. One option discussed earlier involves DNS redirection to a server capable of logging keystrokes. Even then, an adversary would need to wait until the user attempted to login and hope that the server authentication warning is ignored. Remote brute force is also an option, but extremely noisy and requires a presense online, which in easier to detect. This makes password sniffing and guessing difficult.
Furthermore, a private key can be brute forced off-line if it is encrypted with a passphrase, and no one would know it was being conducted. This is assuming the private key is actually encrypted like it should be, which might be hard to manage and enforce. This type of attack of course would not be possible without somehow gaining access to a user's private key file. Likewise, if an attacker first gains access to a shadow or SAM database, passwords can be brute forced off-line just as easily.
The immediate solution is to apply complexity requirements for the password or passphrase. Users are always resistant to choosing complex passwords, because they're difficult to remember, but at least an operating system can enforce a policy (ie via PAM) for passwords, whereas this is not so easy with key pairs.
Password authentication and public key authentication both utilize cryptography, but in different ways. Using public key, a server dictates the supported algorithms for creating the keys. SSH2 requires DSS and recommends RSA. It will not accept use of any less secure algorithms without custom configuration, however DSS and RSA happen to be quite strong. In other words, it's relatively safe by default. Passwords on the other hand rely on mechanisms offered by the server operating system. Some modern installations still allow password hashing with algorithms based on DES, a completely intolerable system these days. A small number even select DES by default.
While this is certainly not an exhaustive list of pros and cons, it should get some ideas flowing. SSH2 is very flexible and does it's job well, but as previously warned - a small configuration error or weak cryptosystem could spoil all of it's goals.
[1]. OpenSSH client and server.
http://www.openssh.org
[2]. RFC Drafts for SSH-ARCH, SSH-TRANS, SSH-AUTH, and SSH-CONN.
http://www.openssh.org/txt/draft-ietf-secsh-architecture-12.txt
http://www.openssh.org/txt/draft-ietf-secsh-transport-14.txt
http://www.openssh.org/txt/draft-ietf-secsh-userauth-15.txt
http://www.openssh.org/txt/draft-ietf-secsh-connect-15.txt
[3]. Ethereal Protocol Analyzer.
http://www.ethereal.com
[4]. Barrett, Daniel J. and Richard E. Silverman. SSH, The Secure Shell: The Definitive Guide.
USA: O'Reilly Media, Inc. 2005.
http://www.oreilly.com/catalog/sshtdg/
[5]. Snader, Jon C. VPNs Illustrated - Tunnels, VPNs, and IPsec.
USA: Person Education / Addison Wesley. 2006.
http://www.awprofessional.com/bookstore/product.asp?isbn=032124544X&rl=1
[6]. Ferguson, Niels and Bruce Schneier. Practical Cryptography.
Indianaplois, Indiana: Niels Ferguson and Bruce Scheier / Wiley Publishing, Inc.
http://www.schneier.com/book-practical.html